Sia la storia che la didattica della fisica sono piene di esempi non lineari, tanto che si è portati a credere che i sistemi non lineari siano un'eccezione. Ma è vero piuttosto il contrario!

Nella realtà i sistemi non lineari sono la regola e i fenomeni caotici sono estremamente frequenti.

Sono tanti gli esempi di caos presenti nel mondo reale: il tempo meteorologico, la formazione delle nuvole, la fibrillazione del cuore umano, la turbolenza nel flusso dei fluidi, il movimento di un semplice pendolo attratto da alcuni magneti, le oscillazioni delle azioni della borsa valori, la configurazione delle linee costiere, il moto dei satelliti di forma irregolare, le traiettorie dei meteoriti, l'orbita irregolare di Plutone, la formazione degli anelli di Saturno, il moto turbolento della Grande Macchia Rossa di Giove, le variazioni nelle popolazioni di animali, la propagazione dei virus (AIDS), le scariche elettriche dei neuroni del cervello, il gocciolamento di un rubinetto, le traiettorie irregolari del volo a zig-zag di una mosca, il movimento degli occhi nei schizofrenici, le transizioni di fase dei corpi, la formazione dei fiocchi di neve, eccetera.

Vediamo in dettaglio qualcuno di questi esempi:

• il pendolo
• la ruota idraulica
• il rubinetto gocciolante
• il tempo meteorologico
• il sistema solare

CAOS E PENDOLI

Anche in un sistema apparentemente semplice esiste il caos.

Esistono sistemi apparentemente semplici, trattabili con equazioni semplici, in cui però è praticamente impossibile determinarne il comportamento futuro. Uno di questi è un pendolo composto da un filo a cui è appesa una sferetta di ferro; sul piano orizzontale sotto il pendolo sono disposte tre calamite uguali, poste ai vertici di un triangolo equilatero. Se lasciamo andare la sferetta da una posizione qualsiasi, essa oscillerà in maniera irregolare, guidata dalla forza peso e dalle forze magnetiche che la attraggono verso ciascuna delle calamite.

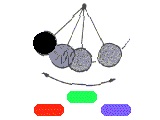
A causa degli attriti finirà poi per fermarsi in una delle tre posizioni di equilibrio possibili, al di sopra di una calamita.

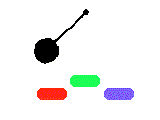
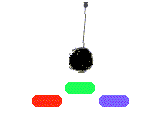
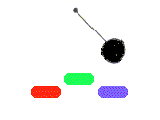
E' possibile predire sopra quale calamita si arresta il pendolo a partire da una posizione iniziale assegnata?
La meccanica classica, essendo deterministica ci farebbe rispondere di sì.

Immaginiamo di osservare il pendolo dall'alto e di assegnare uno di tre colori diversi ad ogni posizione iniziale secondo quale risulta essere la posizione finale (ad esempio rosso per la calamita 1, verde per la calamita 2, blu per la calamita 3), in modo da ottenere un disegno bidimensionale.

Ciò che ci si aspetta di vedere sono tre zone colorate nettamente distinte fra di loro. Non è così! Accanto a zone di colore uniforme si hanno zone ampie di colore non ben definito, in cui i punti colorati si dispongono in strisce e macchie di diverse forme e dimensioni.

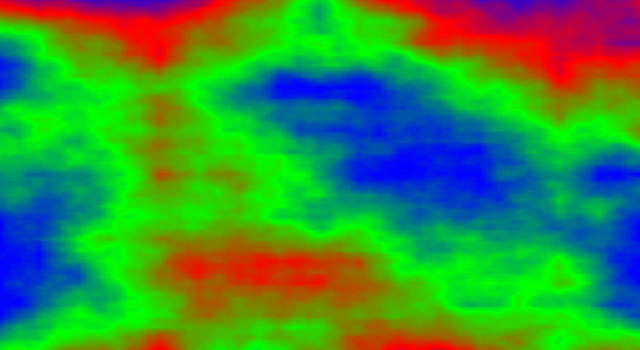
La situazione non migliora nemmeno aumentando la precisione delle misure.

Possiamo simulare facilmente questo tipo di sistemi con l'aiuto di un computer, ma anche qui, per quanto piccoli, siamo in presenza di errori nella determinazione delle posizioni iniziali.

Il CAOS è quindi una conseguenza dell'impossibilità di avere una precisione infinita nella determinazione della posizione iniziale.

Punti che sono molto vicini tra di loro portano a posizioni finali totalmente diverse!

LA RUOTA IDRAULICA DI LORENZ

Secchi che si riempiono e si svuotano possono dare il caos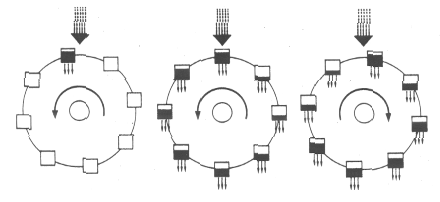

Il primo famoso sistema caotico scoperto da Edward Lorenz corrisponde esattamente ad un dispositivo meccanico: una ruota idraulica. Questo semplice dispositivo si dimostra capace di un comportamento sorprendentemente complicato.

Sopra la parte centrale della ruota idraulica cade dell'acqua ad un ritmo costante.

1. Sopra la parte centrale della ruota idraulica cade dell'acqua ad un ritmo costante. Se il flusso dell'acqua che va a cadere nel secchio alla sommità della ruota è lento, il secchio non si riempie mai abbastanza per superare l'attrito, e la ruota non comincia mai a girare.
2. Se il flusso è più veloce, il peso del secchio in alto mette in movimento la ruota. La ruota idraulica inizia un movimento che continua a velocità costante.
3. Se però il flusso è ancora più veloce, la rotazione diventa caotica, a causa degli effetti non lineari intrinseci al sistema. Quando i secchi passano sotto la caduta d'acqua, in quale misura si riempiono dipende dalla velocità della rotazione. Se la ruota sta girando rapidamente, i secchi hanno poco tempo per riempirsi. Inoltre, se la ruota gira rapidamente i secchi possono salire dall'altra parte prima di avere avuto il tempo di svuotarsi completamente. Di conseguenza, il peso dell'acqua contenuta nei secchi che stanno risalendo farà prima rallentare e poi diminuire la rotazione. In effetti, come scoprì Lorenz, su lunghi periodi la rotazione può invertirsi molte volte, non passando mai a una velocità costante e non ripetendosi mai in modo prevedibile.



1. Punto fisso



2. Ciclo limite



3. Attrattore strano



Diagramma di biforcazione

IL CAOS NEL RUBINETTO CHE GOCCIOLA

Il comportamento delle gocce può essere di tipo caotico.



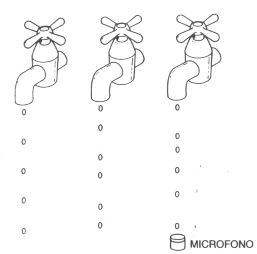
Molti sanno che le gocce che cadono da un rubinetto che gocciola presentano un andamento periodico. L'intervallo fra due gocce successive può essere regolarissimo, e molti, nelle notti di insonnia, sono stati con l'orecchio teso ad aspettare che cadesse la goccia successiva. Meno noto è il comportamento di un rubinetto quando la velocità del flusso è un po' più elevata. Si può spesso individuare un regime in cui in cui le gocce, pur cadendo sempre separate, cadono con un ritmo che non si ripete mai, come un tamburo che improvvisi cadenze sempre nuove. E' un esperimento che chiunque può effettuare facilmente; i rubinetti senza frangigetto funzionano meglio. Facendo cadere le gocce da un normale rubinetto su un microfono è possibile registrare i corrispondenti impulsi sonori.

Un grafico in cui gli intervalli fra le gocce siano riportati a coppie è uno strumento efficace per ricavare una sezione dell'attrattore soggiacente.

Il risultato più interessante dell'esperimento è che nel regime non periodico si trovano attrattori caotici.

Il fatto che nei grafici compaiono delle strutture dimostra che l'aleatorietà possiede una base deterministica.

In particolare molti gruppi di dati hanno una forma a ferro di cavallo.



IL CAOS CHE CHIAMIAMO TEMPO METEOROLOGICO

Una farfalla sbatte le sue ali nella foresta del Sud America, può causare un uragano in Cina.





Le previsioni del tempo fanno parte di ogni notiziario. Vengono date per tre, forse quattro giorni. E talvolta non sono nemmeno esatte! Ma perché non si possono dare per una settimana, o per un mese?

Ci sono molte variabili associate al tempo: temperatura, pressione dell'aria, velocità del vento, direzione del vento, umidità e molte altre. Le equazioni che governano il tempo coinvolgono tutte queste variabili.

Si possono mettere accuratamente tutte queste variabili in un'equazione e calcolare, con qualche grado di incertezza il valore di tutte le variabili al secondo passo. Questi risultati possono essere rimessi nell'equazione e trovare dunque i valori al passo successivo. Lasciamo al computer il compito di eseguire le iterazioni per un tempo sufficientemente lungo e sapremo che tempo farà tra un mese. O no?



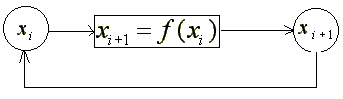
Un meteorologo, Edward Lorenz, provò a farlo. Lorenz decise di far girare il programma più a lungo. Per far questo utilizzò due sistemi. Prima lasciò che ci pensasse il computer, successivamente immise i valori troncati alla terza cifra decimale contro le sei disponibili. Il risultato fu che le due conclusioni furono completamente differenti. La differenza di uno su mille era abbastanza per cambiare significativamente l'output.



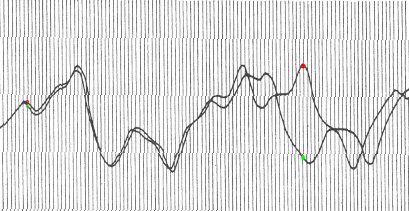
E' quella che si chiama dipendenza sensibile dalle condizioni iniziali. In termini di tempo, questo significa che il caos limita il periodo di tempo in cui si possono fare previsioni meteorologiche!

Lorenz coniò il termine Effetto Farfalla per descrivere questa sensibilità allo stato di partenza del processo.

IL CAOS NEL SISTEMA SOLARE

L' Universo non è un gigantesco orologio, infatti nel Sistema Solare esiste il caos.



Il capitombolare caotico di Hyperion



Il capitombolare caotico di Hyperion, uno dei satelliti più distanti di Saturno, con un'orbita di periodo 21 giorni, offre uno dei più drammatici esempi fisici di comportamento caotico.

La causa principale del comportamento di Hyperion è la sua forma irregolare, oltre ad una grande eccentricità nell'orbita. La forma irregolare del satellite soggetto ad una attrazione gravitazionale non uniforme, causa un momento torcente, che è oltretutto fortemente dipendente dal tempo a causa dell'elevata eccentricità dell'orbita.

La rivoluzione caotica di Hyperion è ben illustrata in un modello semplificato. In questo modello l'orbita di Hyperion è supposta essere un'ellisse; il periodo di rotazione è molto più corto del periodo dell'orbita; l'asse di rotazione viene supposto essere perpendicolare al piano dell'orbita. Ne risulta un'equazione del moto ad un solo grado di libertà, che ha come variabile un angolo, che è quella di un pendolo. Analizzando questa equazione si trovano zone caotiche abbastanza ampie che hanno attitudine all'instabilità.

I satelliti di Marte



Phobos, un satellite di Marte, è di forma irregolare come Hyperion, ma la sua eccentricità dell'orbita è invece bassa, come anche Deimos, l'altro satellite di Marte, che ha un'eccentricità dell'orbita veramente piccola. Tuttavia, compiendo un'analisi della stabilità simile a quella per Hyperion, risulta che la zona caotica non è per niente microscopica. Anche questa zona caotica ha attitudine di instabilità, come Hyperion.

Tutti i satelliti di forma irregolarmente non sferica che ruotano sincronizzati devono aver trascorso un periodo di tempo capitombolando caoticamente. Il tempo che hanno trascorso in queste condizioni deve essere comparabile con il tempo di aggiustamento della rotazione.

Il gap di Kirkwood



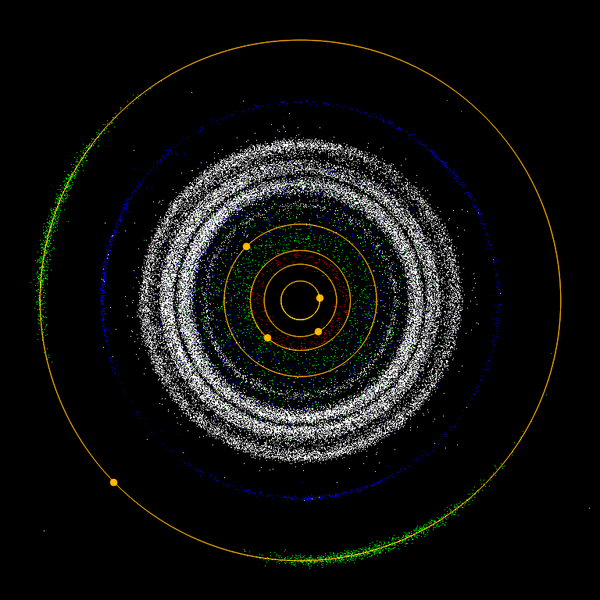
La distribuzione del semiasse maggiore degli asteroidi non è uniforme; ci sono parecchi gap. Mediante simulazione numerica effettuata su lunghi periodi di tempo, si è osservato che le orbite degli asteroidi subiscono una variazione dell'eccentricità nel tempo.

Nel corso di milioni di anni periodi caratterizzati da alta eccentricità sono intervallati da periodi di bassa eccentricità e tali variazioni sembrano succedersi ad intervalli irregolari. In entrambi i casi la caratteristica delle traiettorie è di tipo caotico. I grandi incrementi di eccentricità sono importanti per la formazione dei gap perché nella locazione dei gap le eccentricità maggiori di 0.3 incrociano l'orbita del pianeta Marte. Gli asteroidi di questo tipo possono essere rimossi da incontri ravvicinati o collisioni con Marte.

Il trasporto di meteoriti



Non è ancora ben chiara l'origine di questi sassi che contengono molte informazioni circa la formazione del sistema solare. Si ritiene abbiano origine nella cintura degli asteroidi, ma ciò che manca è un meccanismo dinamico che sia in grado di prevederne la formazione.

Tuttavia esistono simulazioni numeriche di tipo casuale che prevedono moto tridimensionale e che includono variazioni dell'orbita del pianeta Giove come risulta dalle perturbazioni degli altri pianeti, danno come risultato asteroidi con orbite caotiche di grande eccentricità che possono attraversare l'orbita della Terra e dare collisioni dirette.

I pianeti esterni e Plutone



Il Sistema Solare è stabile? La stabilità dell'attuale Sistema Solare rimane sconosciuta. Certamente la grande età del Sistema Solare porterebbe a pensare che lo sia, ma piccole instabilità potrebbero essere ancora presenti. Ad esempio nel moto degli asteroidi piccole instabilità possono portare ad improvvisi cambiamenti dell'orbita.

Il moto di Plutone è straordinariamente complicato. L'orbita di Plutone è unica tra i pianeti. E' sia eccentrica (e=0.25) che inclinata (i=16°). Le orbite di Nettuno e Plutone si incrociano, tuttavia la risonanza assicura che i due pianeti non si avvicinino mai. Esaminando la variazione dell'inclinazione di Plutone nell'arco di milioni di anni non risultano esserci periodicità per cui si pensa che il comportamento sia caotico, anche se il periodo di tempo considerato potrebbe essere ancora breve.

La Grande Macchia Rossa di Giove



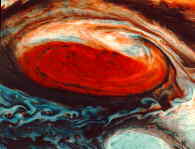
Si tratta di un grande ovale vorticoso, di una tempesta gigantesca che non si muove e non si esaurisce mai. Il pianeta gigante ha una rotazione rapida, col periodo di 10 ore terrestri. La grande velocità di rotazione produce una grande forza di Coriolis, la forza laterale che spinge una persona che cammini attraverso una giostra, e la forza di Coriolis mantiene in movimento la macchia.

Utilizzando le leggi della dinamica si può dunque sviluppare un modello matematico, fatto di equazioni non lineari, di questo sistema meteorologico extraterrestre ed eseguirne una simulazione su computer. Ne risulta che la macchia è un sistema che si auto-organizza, creato e regolato dalle stesse variazioni non lineari che creano la turbolenza imprevedibile attorno ad essa. E' un caos stabile.